Angular Distance Between Two Stars

Angle between the two sightlines or two objects as viewed from an observer

Angular altitude $\theta$ (besides known as angular separation, apparent distance, or credible separation) is the angle between the two sightlines, or between 2 point objects as viewed from an observer.

Angular altitude appears in mathematics (in particular geometry and trigonometry) and all natural sciences (e.1000. astronomy and geophysics). In the classical mechanics of rotating objects, information technology appears alongside angular velocity, angular acceleration, angular momentum, moment of inertia and torque.

Utilize [edit]

The term athwart distance (or separation) is technically synonymous with bending itself, but is meant to suggest the linear distance betwixt objects (for instance, a couple of stars observed from World).

Measurement [edit]

Since the athwart distance (or separation) is conceptually identical to an angle, information technology is measured in the same units, such equally degrees or radians, using instruments such as goniometers or optical instruments specially designed to point in well-defined directions and record the corresponding angles (such as telescopes).

Equation [edit]

General case [edit]

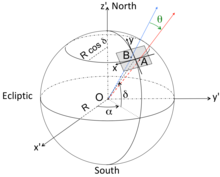
Athwart separation $\theta$ between points A and B as seen from O

To derive the equation that describes the angular separation of two points located on the surface of a sphere as seen from the center of the sphere, nosotros employ the example of two astronomical objects $A$ and $B$ observed from the Earth. The objects $A$ and $B$ are divers by their celestial coordinates, namely their correct ascensions (RA), $(\blastoff _{A},\alpha _{B})\in [0,2\pi ]$ ; and declinations (december), $(\delta _{A},\delta _{B})\in [-\pi /two,\pi /2]$ . Let $O$ indicate the observer on Globe, assumed to exist located at the center of the celestial sphere. The dot production of the vectors $\mathbf {OA}$ and $\mathbf {OB}$ is equal to:

\mathbf {OA} \cdot \mathbf {OB} =R^{two}\cos \theta

which is equivalent to:

\mathbf {n_{A}} .\mathbf {n_{B}} =\cos \theta

In the $(10,y,z)$ frame, the two unitary vectors are decomposed into:

\mathbf {n_{A}} ={\brainstorm{pmatrix}\cos \delta _{A}\cos \alpha _{A}\\\cos \delta _{A}\sin \alpha _{A}\\\sin \delta _{A}\terminate{pmatrix}}\mathrm {\qquad and\qquad } \mathbf {n_{B}} ={\begin{pmatrix}\cos \delta _{B}\cos \alpha _{B}\\\cos \delta _{B}\sin \blastoff _{B}\\\sin \delta _{B}\stop{pmatrix}}.

Therefore,

\mathbf {n_{A}} \mathbf {n_{B}} =\cos \delta _{A}\cos \alpha _{A}\cos \delta _{B}\cos \alpha _{B}+\cos \delta _{A}\sin \alpha _{A}\cos \delta _{B}\sin \alpha _{B}+\sin \delta _{A}\sin \delta _{B}\equiv \cos \theta

then:

\theta =\cos ^{-1}\left[\sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\cos(\alpha _{A}-\alpha _{B})\correct]

Small angular distance approximation [edit]

The above expression is valid for any position of A and B on the sphere. In astronomy, it often happens that the considered objects are really close in the sky: stars in a telescope field of view, binary stars, the satellites of the behemothic planets of the solar system, etc. In the case where $\theta \ll 1$ radian, implying $\alpha _{A}-\alpha _{B}\ll 1$ and $\delta _{A}-\delta _{B}\ll 1$ , nosotros can develop the above expression and simplify it. In the small-angle approximation, at second gild, the higher up expression becomes:

\cos \theta \approx i-{\frac {\theta ^{2}}{2}}\approx \sin \delta _{A}\sin \delta _{B}+\cos \delta _{A}\cos \delta _{B}\left[ane-{\frac {(\alpha _{A}-\blastoff _{B})^{2}}{2}}\right]

meaning

1-{\frac {\theta ^{2}}{ii}}\approx \cos(\delta _{A}-\delta _{B})-\cos \delta _{A}\cos \delta _{B}{\frac {(\blastoff _{A}-\alpha _{B})^{ii}}{2}}

hence

1-{\frac {\theta ^{2}}{ii}}\approx 1-{\frac {(\delta _{A}-\delta _{B})^{ii}}{ii}}-\cos \delta _{A}\cos \delta _{B}{\frac {(\blastoff _{A}-\alpha _{B})^{2}}{2}}

Given that $\delta _{A}-\delta _{B}\ll 1$ and $\alpha _{A}-\alpha _{B}\ll 1$ , at a second-order evolution it turns that $\cos \delta _{A}\cos \delta _{B}{\frac {(\alpha _{A}-\alpha _{B})^{2}}{two}}\approx \cos ^{ii}\delta _{A}{\frac {(\alpha _{A}-\blastoff _{B})^{2}}{2}}$ , then that

\theta \approx {\sqrt {\left[(\alpha _{A}-\alpha _{B})\cos \delta _{A}\right]^{ii}+(\delta _{A}-\delta _{B})^{2}}}

Pocket-size angular distance: planar approximation [edit]

Planar approximation of athwart altitude on sky

If we consider a detector imaging a small sky field (dimension much less than one radian) with the $y$ -centrality pointing upward, parallel to the meridian of right rising $\alpha$ , and the $x$ -axis along the parallel of declination $\delta$ , the angular separation tin be written as:

\theta \approx {\sqrt {\delta x^{2}+\delta y^{2}}}

where $\delta x=(\blastoff _{A}-\alpha _{B})\cos \delta _{A}$ and $\delta y=\delta _{A}-\delta _{B}$ .

Note that the $y$ -axis is equal to the declination, whereas the $x$ -axis is the correct ascension modulated past $\cos \delta _{A}$ because the department of a sphere of radius $R$ at declination (latitude) $\delta$ is $R'=R\cos \delta _{A}$ (run into Figure).