How To Calculate Resultant Vector

The resultant vector is the vector that 'results' from adding two or more vectors together. In that location are a 2 different ways to calculate the resultant vector.

Methods for calculating a Resultant Vector:

The head to tail method to calculate a resultant which involves lining upwardly the caput of the one vector with the tail of the other.
The parallelogram method to calculate resultant vector. This method involves properties of parallelograms but, in the end, boils downward to a elementary formula.

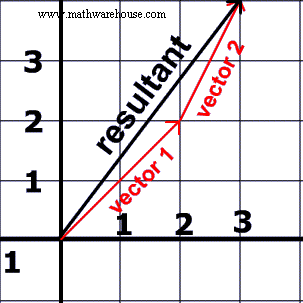
picture of resultant vector

In the picture on the left, the black vector is the resultant of the two red vectors. To effort to understand what a resultant is consider the following story.

If y'all drove from your business firm, centered at the origin. To your friends firm, at the signal (3, 4), imagine that you had to take two dissimilar roads these are the two cherry-red vectors. Notwithstanding, the resultant vector vector would be the straight line path from your home to your friend's house, and the blackness vector represents that path.

Caput to Tail Method

The head to tail method is way to find the resultant vector. The steps are quite straight forward. The head to tail method considers the head of a vector to exist the cease with the arrow, or the 'pointy terminate'. The tail of the vector is where the vector begins.

Place the ii vectors next to each other such that the head of the one vector is touching the tail of the other vector.
Draw the resultant vector past starting where the tail of commencement vector is to the head of second vector.

Steps for Head to Tail Method

head to tail method animated gif

Summate the magnitude resultant vector

Detect the sum of each pair of vectors (the magnitude of the resultant vector).

picture of resultant vector

Do Bug

Problem i

You left your business firm to visit a friend. You lot got in your car drove 40 miles east, then got on a highway and went l miles northward.

Draw a vector from the kickoff of your journeying, your home, and the stop, your friend's house.

Resultant Vector Real world problem

How long is the vector that yous drew?

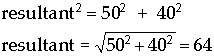
resultant answer

Problem 2

What is the sum of the two vectors? Use the head to tail method to calculate the resultant vector in the motion picture on the right.

Head to Tail Practice

Parallelogram Method to Calculate Resultant

Before tackling the parallelogram method for solving resultant vectors, you should be comfortable with the following topics.

SOHCAHTOA (basic sine, cosine, tangent)
Law of Cosines
Law of Sines
The Following Properties of Parallelograms

Contrary Sides of Parallelograms are Congruent
Opposite Angles of Parallelograms are Congruent

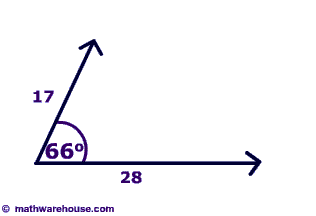
Trouble 3

To best understand how the parallelogram method works, lets examine the two vectors below. The vectors have magnitudes of 17 and 28 and the angle between them is 66°. Our goal is to utilise the parallelogram method to determine the magnitude of the resultant.

Footstep 1

Describe a parallelogram based on the two vectors that y'all already accept. These vectors will be ii sides of the parallelogram (not the reverse sides since they have the angle between them).

Step 2

We now take a parallelogram and know two angles (contrary angles of parallelograms are congruent). We tin also effigy out the other pair of angles since the other pair are coinciding and all four angles must add upwardly to 360.

Step 3

Draw the paprallelograms diagonal. This diagonal is the resultant vector.

Step 4

Utilize the police force of cosines to determine the length of the resultant.

Apply the law of cosines to calculate the resultant.

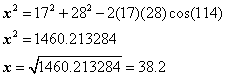
problem 3